Maneuvers

Impulsive maneuver

The simplest maneuver model is ImpulseManeuver. This models an instantaneous velocity change. As the change is a discrete event, it is implemented as an EventDetector with an event handler that return Action.RESET_STATE when the event occurs, so the resetState method can be called and change the spacecraft velocity.

As ImpulseManeuver is really an EventDetector and relies on resetState, it can be used with most propagators (analytical propagators, semi-analytical propagators or numerical propagators). It cannot be used with TLE propagators or ephemeris-based propagators because they forbid state resets.

The ImpulseManeuver is built from a lower level EventDetector that acts as a trigger for the maneuver. Any detector can be used. Classical ones are DateDetector for maneuvers with already known dates, but it is possible to use for example NodeDetector to perform inclination maneuvers at nodes or PositionAngleDetector to perform circularization maneuvers at apogee.

The other build parameters for ImpulseManeuver are the ΔV vector in spacecraft frame (typically one of the canonical spacecraft axis depending on the thruster used for this maneuvers) and the specific impulse (which is used to update the mass). The ΔV vector will be converted from spacecraft frame to inertial frame taking into account either the current attitude as configured in the propagator or an overriding attitude provider. Overriding the attitude allows to configure the nominal attitude in the propagator while using a maneuver-specific attitude just for the sake of ΔV vector computation.

Continuous thrust maneuver

The most accurate maneuver model is Maneuver. This models a progressive velocity change induced by firing a thruster. As the change is a continuous one, it is implemented as a ForceModel.

As Maneuver is really a ForceModel, it can be used only with integration-based propagators (semi-analytical propagators with some care and numerical propagator). Using it with semi-analytical propagators is limited, though. Large maneuvers or long maneuvers that extend to a sizeable portion of the orbit may break the assumptions used to separate mean motion from short periodic terms.

The following class diagram shows the design of the Maneuver class and supporting classes and interfaces.

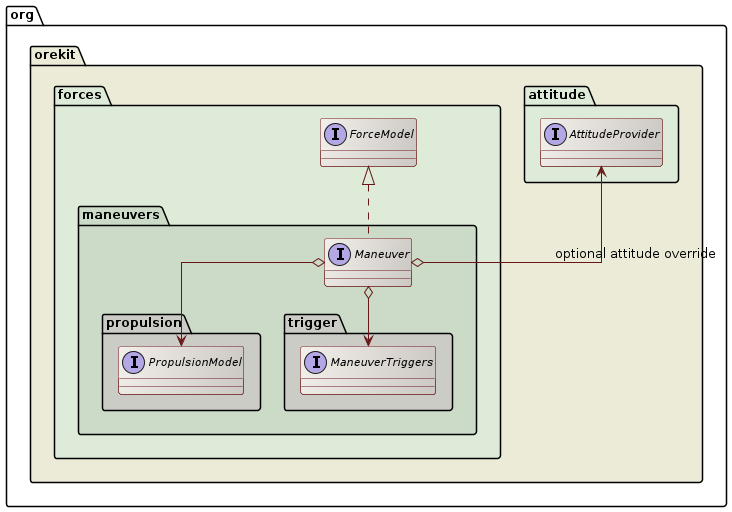
A Maneuver contains a PropulsionModel, a ManeuverTriggers and an optional attitude override.

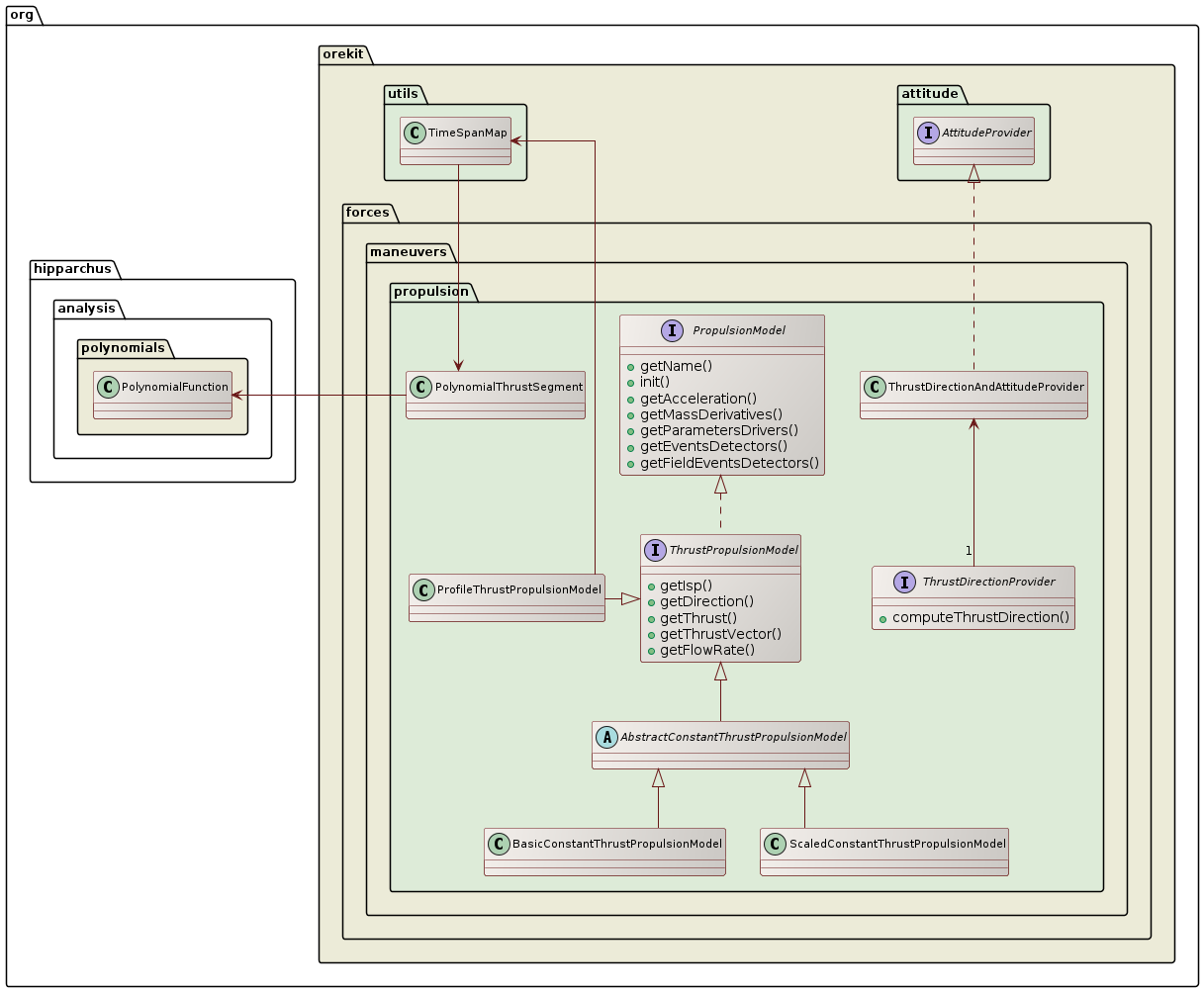
The PropulsionModel defines the characteristics of the acceleration. Its main implementation is BasicConstantThrustPropulsionModel. The ScaledConstantThrustPropulsionModel implementation is intended to be used in estimation processes, by evaluating scaling factors. The ProfileThrustPropulsionModel provides a piecewise-polynomial thrust with constant specific impulse that can model profile-based thrusts.

The ManeuverTriggers defines when the acceleration occurs. There are two main implementations: IntervalEventTrigger and StartStopEventsTrigger. IntervalEventTrigger is based on a single event detector, firing intervals correspond to time spans with positive value of the single event detector g function. StartStopEventsTrigger is based on a pair of event detectors, firing intervals starts when the start detector g function becomes positive and stops when the stop detector g function becomes positive. The decreasing events of both detectors (i.e. when their g functions become negative) are ignored.

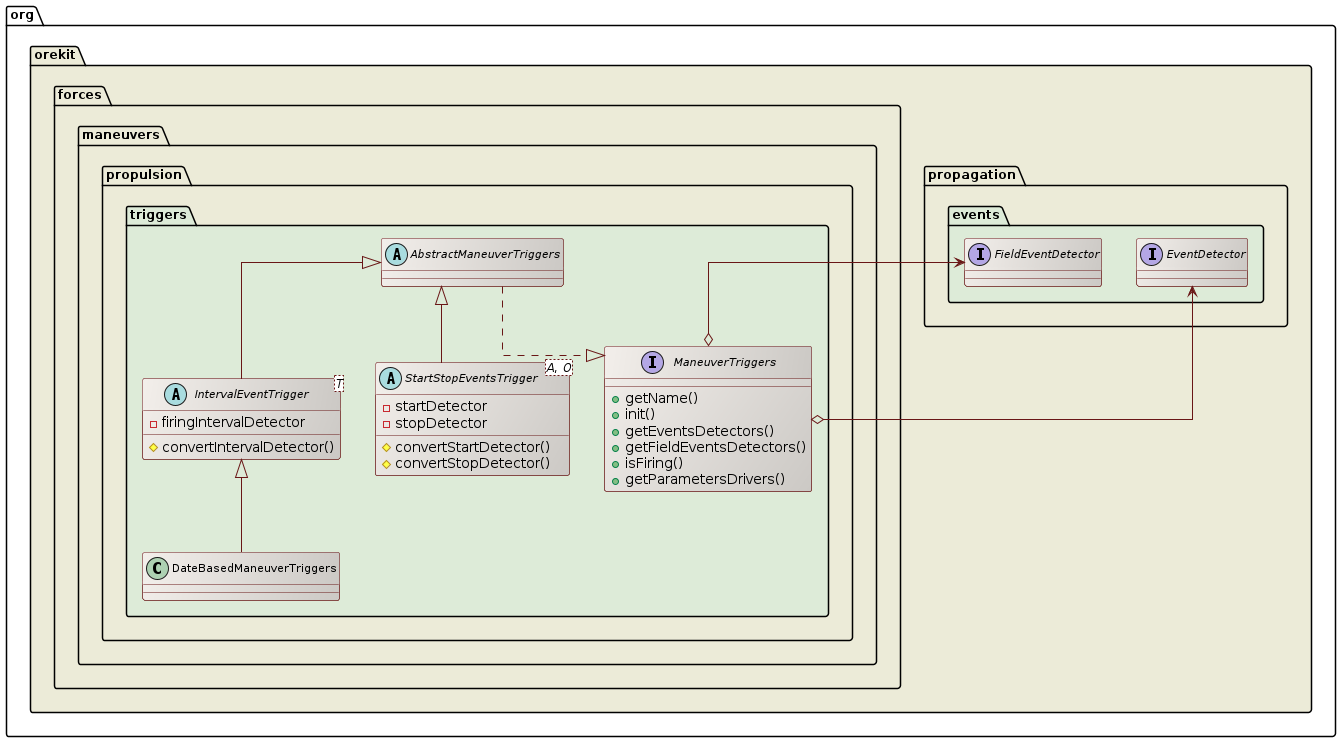
In order to allow field-based propagation, both IntervalEventTrigger and StartStopEventsTrigger classes are abstract classes and concrete subclasses must implement a conversion method to automatically generate a field-based event detector from the primitive double based detector provided at construction time for any field. This may be tricky to do and Java syntax is sometimes abstruse with parameterized classes and methods. The following code snippet shows how to do it for an arbitrary XyzDetector for which a field-based implementation FieldXyzDetector exists. In this example, we assume the detector is built from a date and a number parameter and we use it in IntervalEventTrigger. The pattern for StartStopEventsTrigger is similar, except that two methods must be implemented: convertStartDetector and convertStopDetector.

public XyzTrigger extends IntervalEventTrigger<XysDetector> {

    protected <D extends FieldEventDetector<S>, S extends CalculusFieldElement<S>>
        FieldAbstractDetector<D, S> convertIntervalDetector(final Field<S> field, final XyzDetector detector) {
 
         final FieldAbsoluteDate<S> date  = new FieldAbsoluteDate<>(field, detector.getDate());
         final S                    param = field.getZero().newInstance(detector.getParam());
 
         @SuppressWarnings("unchecked")
         final FieldAbstractDetector<D, S> converted = (FieldAbstractDetector<D, S>) new FieldXyzDetector<>(date, param);
         return converted;
     }

 }

Small maneuver

The SmallManeuverAnalyticalModel is another maneuver model intended to be used for fast optimization of a large number of small station-keeping maneuvers at once.

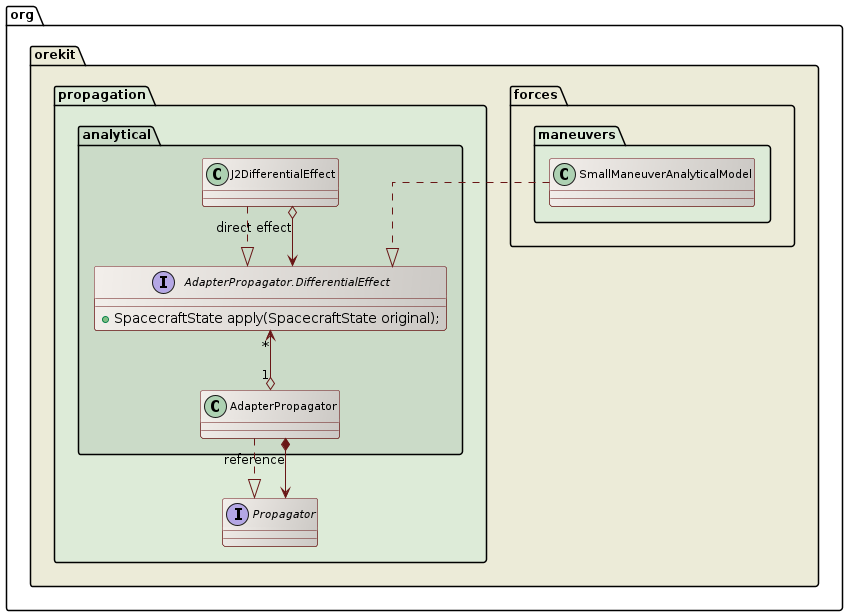
The principle of this model is to run a full-featured propagator without maneuvers first and have it generate a reference ephemeris. Then, at each iteration of an optimization loop, an AdapterPropagator is created and populated with the differential effects induced by the maneuvers that should be added to the reference ephemeris. The maneuvers created change from iteration to iteration as their parameters are optimized. Then the AdapterPropagator is run and the station keeping targets are checked. As the differential effects are analytical and as the reference ephemeris, once generated, is also analytical, this propagation loop is much faster than using the full-featured propagator itself during optimization.

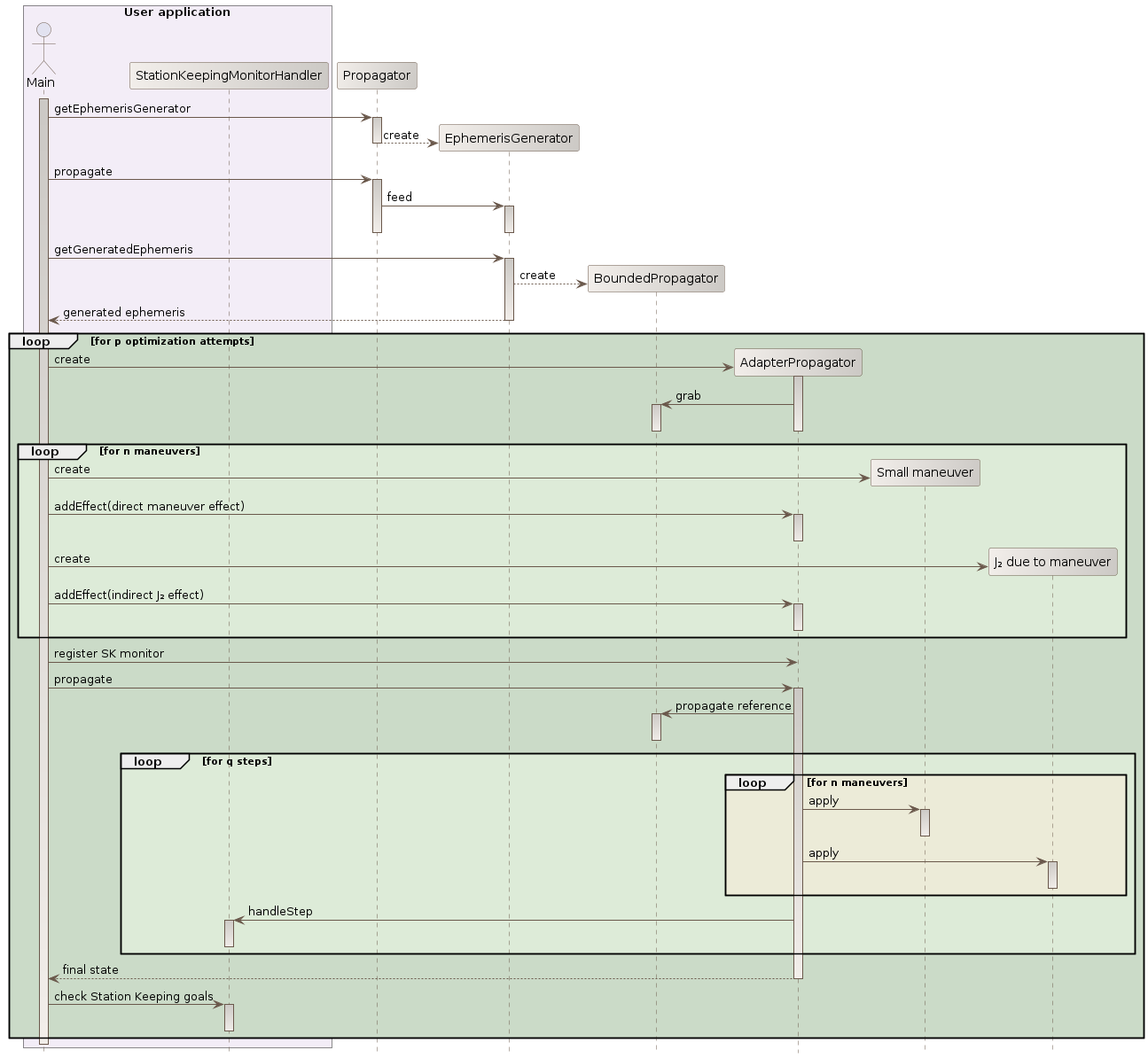
Of course, once the maneuvers parameters have been optimized, a new full-featured propagation can be performed with maneuvers taken into account for full accuracy.